NB. Probability is complicated, there is obviously much, much more to discuss than this, but the general principles in this article can be applied to your Warhammer games, and to your mindset surrounding “poor” dice rolls.

As the main character, I often think to myself:

• Why does my opponent make all their armour saves, and I don’t?
• How come the Night Lords detachment is shit again?
• I want to put Lilith’s feet in my mouth
• I should have rolled at least 2 6’s on Overwatch, but I rolled zero.

I should have, but should I have had?

When playing Warhammer, we often want our dice to do certain things. We want to make 9″ charges out of deepstrike, but the odds of that are relatively low. We want to make all of our 4+ invulnerable saves, and if you’re my opponent, the odds of that are 100%. However, it’s simple enough to say that a 4+ invuln has a 50% chance of being successful, but what is the variance surrounding that?

Firstly, just to prove that rolling a 4+ on a single D6 really is 50% odds, and give a little bit of understanding of the probability we will be talking about:

• A D6 has 6 outcomes, 1, 2, 3, 4, 5, 6.
• Each outcome has a 16.66% chance of occurring (1/6*100).
• To roll a 4+, there are 3 possible outcomes, 4, 5, 6.
• If we add these together, we get 16.66% * 3 = 50%.

But what we want to find out is, how often are the odds of rolling a 4+ on a D6 dice really 50%?

Odds are great to understand in a dice game, because they can help inform our decisions and guide us towards the correct path forwards. But as I’m sure all of you have experienced firsthand, there is variance to these odds.

Before we get started, lets define expectation, variance, and standard deviation.

• Expectation (expected value or mean) gives us a single value that summarizes the average outcome, this is often represented by some measure of the centre of a probability distribution.
• Variance quantifies how variable the outcomes are about – or around – the average. A low variance suggests that most of the outcomes are close to the expected value, while a high variance would have them spread out.
• Standard deviation tells us by how much a value differs from the mean of a group. 68% of values fall within one standard deviation of the mean, 95% within two, and 99.7% within 3. It essentially tells us the amount of variation we can expect.

We can represent the expectation of a discrete random variable X as E(X) and variance as Var(X). They can be defined using the following equations (I don’t know how to type mathematical notation in wordpress so enjoy pictures x):

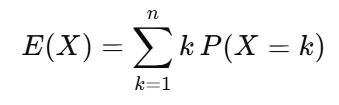
Expectation is a sum of outcomes weighted by their probability.

• X is a random variable that can take values, 1, 2, … n
• P(X = k) is the probability that X takes the value k
• The expected value is the weighted average of all possible outcomes, where each outcome is weighted by its probability.
• Simply put: multiple each possible value of X (each dice face) by it’s probability (1/6), then sum them all up.

Example – 6-sided dice

• As previously stated, there are 6 possible outcomes: 1, 2, 3, 4, 5, 6
• Each has probability P(X = k) = 1/6

Variance:

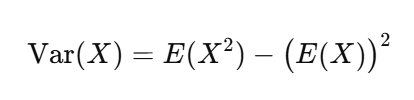
• E(X) = the mean of X
• E(X^2) = the expected value of the square of X
• Var(X) = a measure of how spread out the values of X are around the mean

We already know E(X) = 3.5, the expected value of a D6 – centered around the mean.

For E(X^2) we compute this to 91/6 = 15.7

Computing the variance would leave us with:

Var(X) = E(X^2) – (E(X))^2 = 15.17 – (3.5)^2 = 15.17 – 12.25 = 35/12 = 2.92

From here we can calculate the standard deviation as the square root of 2.92, which is 1.71.

But what does this mean?

The Variance for a single dice roll is equal to 35/12 or 2.92. Variance is a measure of spread: how far values of a random variable typically are from the mean.

For a 6-sided non-toilet dice the mean value is 3.5, the variance tells us how much, on average, each roll differs squared from 3.5. We can make this easier to interpret by finding the standard deviation – taking the square root of the variance – which is in the same units as the expected value. This is 1.71.

Meaning, when rolling a single dice, the expected mean value is 3.5, but it can be expected to be 1.7 away from the mean – higher or lower.

Well, this isn’t very useful information. Expectations and variances are mostly useless for single dice rolls. Each face on a D6 has an equiprobable chance of being rolled. However, expectations and variances are incredible useful when rolling multiple dice. But we aren’t really interested in variance around the mean value while playing Warhammer. Generally, we have an expected value, i.e. 2+ save, 5+ invuln, and knowing the variance around this could be incredible useful for informing our decisions.

To pass a 5+ invulnerable save, the probability of success is 1/3, as there are two possible outcomes on a D6 which lead to success, while failure is 2/3.

To compute the variance, we can use the Bernoulli random variable, as there are two possible outcomes.

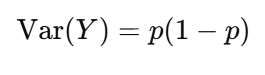
Var(Y) = 1/3(1-1/3) = 0.222

Standard deviation: 0.47

This, again, is of course only data for a single dice roll. What if we applied this to let’s say, 12 dice. As dice rolls are considered independent of each other, we can use a binomial distribution for this calculation. This is a fancy way of saying multiplying the probability by the number of dice.

E(X) = 12 * 1/3 = 4

On average, 4 of them should be a 5+ (5 or 6)

The variance of a binomial is:

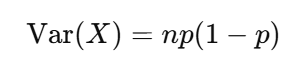
With the standard deviation once again being the square root of the variance.

For 12 dice:

Var(x) = 12*1/3*(1-1/3) = 24/9 = 2.67

Standard deviation is 1.63

So, while we should expect four successes, the actual number will usually be within about +-1.6 of four (so between 2-6 most of the time).

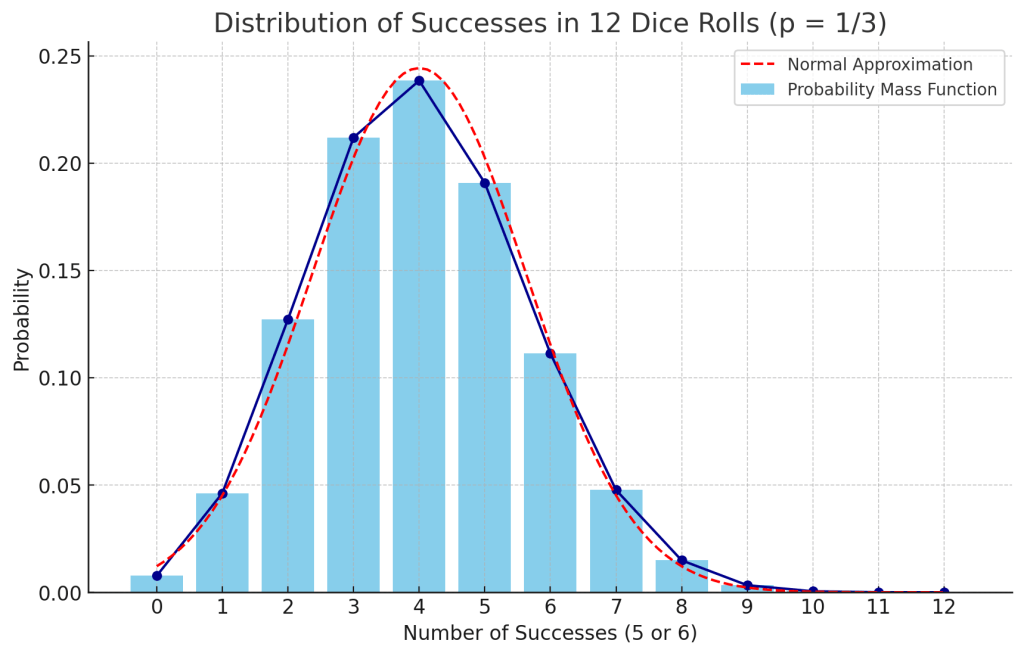
What if we used armour of contempt, so now our save was a 4+?

E(X) = 12 * 1/2 = 6

Var(x) = 12*1/2*(1-1/2) = 3

Standard deviation is 1.73

So, while we should expect six successes, the actual number will usually be within about 1.73 of six (so between 4 and 8 most of the time).

Statistics can be fickle, as I’m sure we have all rolled 10 4+ invulnerable saves before and failed them all! (statistically a 0.0977% probably, or 1/104 chance).

But from these two examples we can take away something I consider to be quite interesting:

• Scenario A: 12 dice, success = 5+ armour save, 6 are passed.
• Scenario B: 12 dice, armour of contempt, success 4+ armour save, 4 are passed.

Consider the previously calculated standard deviations where 68% of all values fall within +-1 standard deviations of the mean. The dice can spike, or they can fail.

The odds of rolling 6 successes on a 5+ armour save, are incredibly close to rolling 4 successes on a 4+, across 12 dice rolls. Using the Z-score for binomial distribution, scenario B represents a scenario 1.225 deviations above the mean, while scenario B is -1.155 below the mean, both being roughly similar – and having about a 11-12% chance of occurring. This, however, is also true of the reverse. Meaning that the odds of rolling 2 successes on a 5+ armour save is also approximately the same odds as rolling 8 4+ across 12 dice rolls, lol.

Variance from the expected mean or why you should stop being a salty bitch

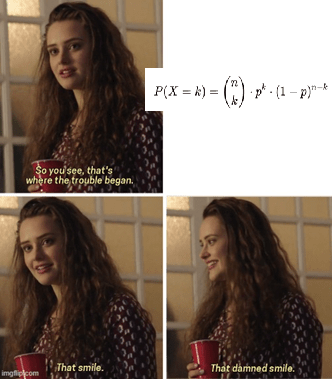
At our core, we are all simple flesh bags with the unfathomable desire of number be good. I just spoke briefly about how there are very similar probabilities of number being bad, and number being good.

This makes me angry.

But what about number being, just ok?

We know, intuitively, without a shadow of a doubt, that a 4+ save is a 50/50. Consider this, the probability of rolling exactly 5 successes on 10 dice, with a 4+ is 24%, with a 37% chance of rolling less, and a 37% chance of rolling more.

Fuck

What about rolling 2 4+ on 4 dice, simple as right? 50/50. No, 37%, however 68% chance of getting >= 2, but also 68% chance of <= 2.

In fact, your odds of getting the average on most dice rolls is about 24%, cool, well for the numbers you’ll be rolling in Warhammer that is.

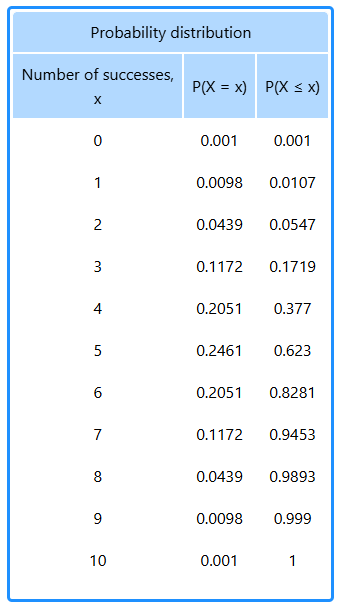
Although our probability of hitting the exact expected odds is about 24%, when we consider the odds of rolling between 4-6 successes, that is increased to about 65% (the standard deviation here being 1.5, so that checks out aye).

Do your own nerd calculations here: Binomial Distribution Probability Calculator

In general, what are the key take aways from this:

• When rolling multiple dice, the expected value gives a good estimate for about where you should expect the outcome to be. The more dice you roll, the more confident you should be that the sum will be close to the expectation. That is not to say that you should increase the number of saving throws you make, in an attempt to get closer to the average.
• You have a pretty good chance – 30%ish – of a roll that sits outside of a single standard deviation from the expected mean, especially with the lowish number of dice regularly rolled in Warhammer.
• We can further elaborate on this to say that if we wanted our standard deviation of successes to be within 10% of the expected number, we would need to roll about 100 dice.

This is all to say that, yes, you will very, very, very frequently experience variance in expected outcome of dice rolls in a game of Warhammer. Even when attempting to minimise the odds and put yourself in favourable positions.

At the end of the day it is a dice game, relax, and enjoy it.

This has been a bit of an unorganised brain dump, but it was fun and interesting to write. Please let me know what I got wrong, I’m sure there is something.

Cya nerds x